Sample Grading scale aligning Marzano’s definition of scales to traditional percents.
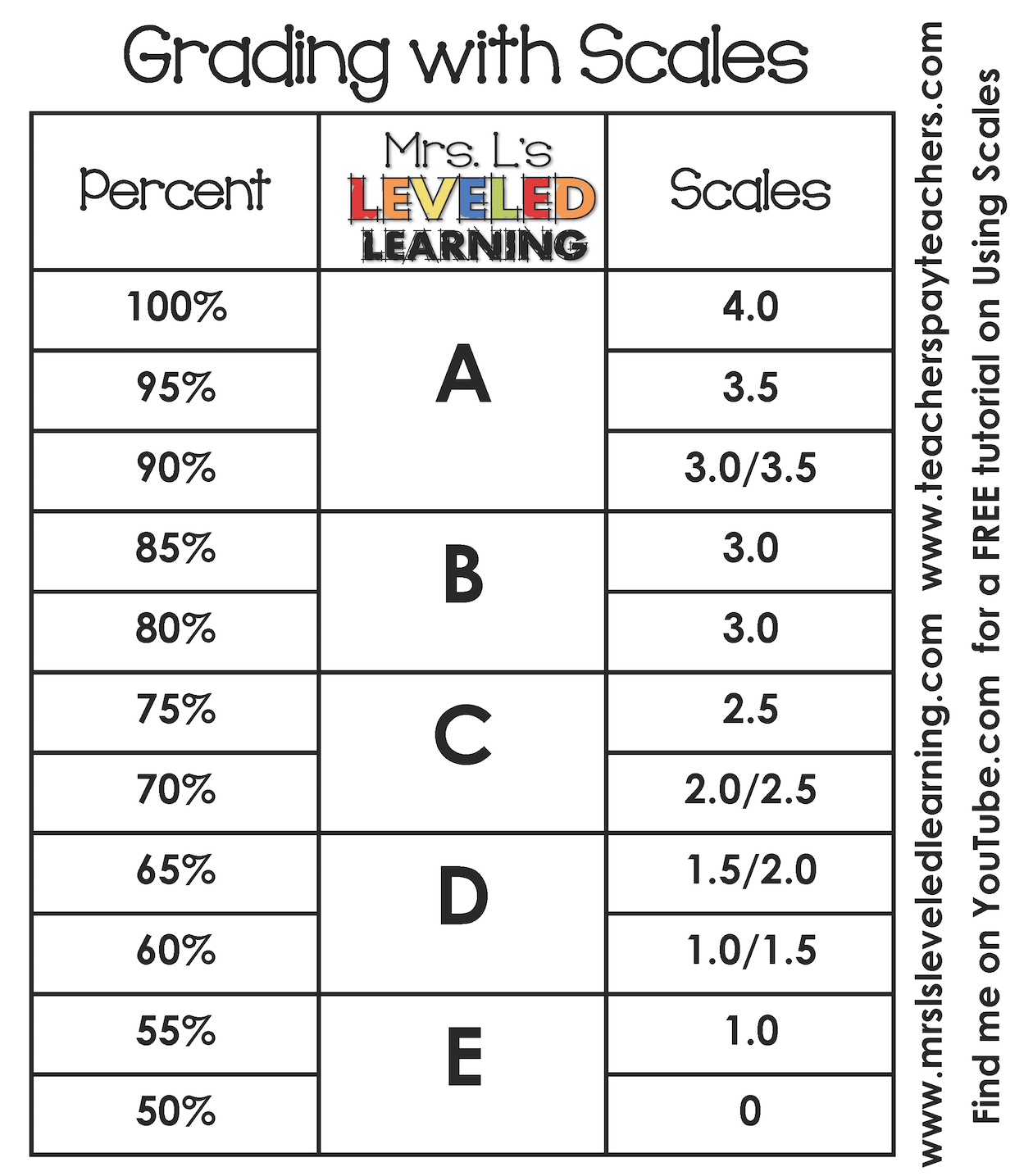
As a classroom teacher, formal grading is an inescapable reality. In the past I have usually assigned points for every problem, and used percentages to assign grades. This fall my district established assigned percentages to correlate with learning scales that simplify the grading process.
4.0 – 100% A+
3.5 – 95% A
3.0 – 90% A-
2.5 – 80% B/B-
2.0 – 70% C/C-
1.5 – 65% D
1.0 – 60% D-
0.0 – 50% E
The first thing I noticed about this percentage assignment is that it isn’t proportional, and that feels a little awkward; but the percentages were chosen based on the intended meaning of each scale. For instance, a student who achieves a 4.0 has gone above and beyond the grade level standard and deserves an A+. A student who achieves a 3.0 has still shown mastery of the grade level standard, and deserves an A. A 2.0 means that the student is approaching grade level mastery, but hasn’t hit it yet, so they would reasonably earn something between a C and B. The rationale for giving 50% as the lowest possible grade is that it has a smaller effect on the overall average than a 0% does. Often it’s unfair to assign a 0% to an assignment for a student who has done okay on most other standards, because it can lower the average score to a point that is impossible to recover from, even if they are trying to improve their grade.
One hiccup I’ve had to work out with my own students is deciding which scale they fall under if they have shown mastery of the 3.0 tasks, but made significant mistakes on the 2.0 tasks. In my Assessments with Learning Goals and Scales, my intention was to create the cognitive tasks in a sequential way so that a student would have to understand the 1.0 tasks in order to perform the 2.0 tasks, or the 2.0 tasks in order to perform he 3.0 tasks, etc. However, some standards are divided based on easier to harder sub skills, not necessarily sequential skills, so at times a student will perform partially in each scale. When this happens I wait to give them full credit for any one section until they redo the problems for the post test.
For instance, in the 5th grade volume standard 5.MD.3, I had students who gave technically correct answers for problems 3g) and 3h) because they correctly counted the units of volume and labeled them “cubic units.” The problem is that in scale 2.0 when I asked them to label the height, length, and width of one cubic unit of volume, they wrote answers like “3 units cubed” and “1 unit.” These mistakes show a misunderstanding of the process of multiplying the 3 dimensions together, or a misunderstanding of the difference between units, square units, and cubed units. How can I give a student a score of 3.0 if I can tell that they really don’t understand the units of volume? Counting cubes is easy, and the standards use the terminology of “cubic units,” but they also need to understand what that means. In the end I decided not to score those students for the pretest attempt, but to teach the concepts related to 1, 2, and 3 dimensional measurement, and assign scores for the post test responses only.
